Учим решать нестандартные задачи с помощью пособий по математике Издательского дома «Федоров»

    Современный человек живет в ситуациях неопределенности и решает множество разнообразных задач. С каждым годом века скоростей информации и технических новинок трудных, проблемных задач становится все больше. Человек должен быть морально готов к осознанному выбору и принятию решений, владеть соответствующими инструментами, и этому нужно учить. Начинать эту работу следует с раннего возраста, включать в любые виды деятельности ребенка как дошкольного, так и школьного возраста. В этом контексте измененные целевые установки и требования к образовательным результатам зафиксированы в различных государственных документах, разработанных стратегиях модернизации российского образования.

    Развитию умственных способностей и личностных качеств младших школьников способствует специально подобранная система задач. В «Концепции развития математического образования в Российской Федерации» (утв. распоряжением Правительства РФ от 24 декабря 2013 г. N 2506) сформулированы приоритетные цели и задачи, обозначены направления и подчеркнуто, что «система учебных программ математического образования в дошкольном и начальном образовании при участии семьи должна обеспечить: широкий спектр математической активности (занятий) обучающихся как на уроках, так и во внеурочной деятельности (прежде всего решение логических и арифметических задач…».

    Курс математики в начальной школе должен для этого иметь необходимые ресурсы и механизмы. Специалисты, занимающиеся проблемами содержания школьного математического образования, обращают внимание авторов программ и учебных пособий на новые целевые установки, ориентируют на активное включение проблемных, творческих, поисковых, эвристических задач, которые принято называть нестандартными.

    Вопросами решения нестандартных задач занимались еще древние египтяне, греки, индийцы, китайцы, арабы. Работы многих математиков, методистов, педагогов посвящались этому: В. Лейбница, П. Ферма, Д. Пойа, Ю.М. Колягина, Л.М. Фридмана и других.

    Конкретной общепринятой классификации нестандартных задач не существует, часто методологи разделяют их на две условные категории, опираясь на работы Б.А. Кордемского (1958) [1]:
1. задачи, примыкающие к школьному курсу математики, но повышенной трудности – типа задач математических олимпиад (логические, комбинаторные и другие);
2. задачи типа математических развлечений (числовые головоломки, ребусы, задачи-шутки, софизмы, задачи на смекалку и др.).

    Задачи подобного типа стимулируют умственные действия, развивают гибкость, неординарность, глубину, критичность мышления, математические и общеинтеллектуальные способности учащихся.

    Ю.М. Колягиным сформулированы критерии оценки качества задач в курсе школьной математики [2]. Среди них выделяются требования к занимательности, новизне, приближенности к возрасту и жизненному опыту ребенка. Такие задачи должны быть интересны для ученика, пробуждать желание действовать, исследовать, думать. Они не должны быть легкими, так как школьник должен испытать радость победы.

    Эмоциональный характер этой работы стимулирует развитие как учебной мотивации, так и мотивации на достижение успеха через преодоление трудностей и проблем в ходе достижения результата. Переживаемая радость от достигнутого результата повышает познавательный интерес. Для решения нестандартных задач учащимся необходимо приложить определенные усилия, проявить волю, настойчивость и целеустремленность, что содействует воспитанию характера. Такие задачи имеют, как правило, необычные формулировки, решаются своеобразными (нешаблонными) приемами.

    Нестандартные задачи обеспечивают усвоение программных знаний на более высоком уровне, возможность выявления способностей и установления уровня развития математического мышления учащихся, проверку способности и умения самостоятельно учиться.

    На протяжении десятилетий педагоги традиционно включают нестандартные задачи в работу: организуют внеклассную работу, различные конкурсы, чемпионаты, математические олимпиады. В последние годы такие задачи используются и при проведении диагностических оценочных процедур, в том числе аттестационных испытаний выпускников начальной школы.

    В 2015 году проводилось Национальное исследование качества образования в начальной школе (НИКО), в содержание работы по математике были включены нестандартные задачи. Анализ результатов выполнения таких диагностических заданий по математике показал, что учащиеся испытывают трудности при решении задач, отличных от шаблонных. Так, при проверке овладения обучающимися основами логического и алгоритмического мышления полностью верно выполняли задание от 20% до 53% участников, а в линии заданий на проверку умений применять математические знания для решения учебно-познавательных и учебно-практических задач, умений решать текстовые задачи с приоритетом заданий повышенного уровня сложности зафиксирован очень низкий процент успешно выполнивших такие задания обучающихся [3].

    Ежегодно нестандартные задачи стали включаться в содержание Всероссийской проверочной работы по математике. Это должно положительно восприниматься педагогами и родителями. Однако опыт методической работы с педагогами показывает обратную ситуацию. Отчасти это можно объяснить тем, что задачи данной категории недостаточно включаются в содержание программ по математике как для учеников, так и в содержание дисциплин в педагогических учебных заведениях. Среди других причин можно выделить отсутствие системных рекомендаций, недостаточность пособий по решению таких задач, дефицит учебного времени на уроках и другие.

    Рассмотрим в обозначенном контексте возможности использования пособий по математике, выпущенных Издательским домом «Федоров».

    Начнем с серии учебных пособий «50 шагов к успеху. Готовимся к Всероссийской проверочной работе». Она включает рабочие тетради для организации комплексной системной подготовки к итоговой диагностической работе (ВПР).

    Обучать приемам решения нестандартных задач нужно при решении арифметических текстовых задач, так как в их сюжетах находят отражение практические ситуации, знакомые ученику, поэтому в рассуждениях он может опираться на свой жизненный опыт. В качестве иллюстрации приведем фрагмент из трех работ пособия обозначенной серии по математике для учащихся 3 классов, автор А.Г. Ефремова. Каждая из предложенных пятидесяти работ содержит два задания и рассчитана на 10–15-минутное включение в урок или внеклассное занятие.

    Задание 2 работы 31 представляет из себя жизненную ситуацию, а данный вид задачи относится к комбинаторным задачам. Задача 1 работы 32 также приближена к практическому жизненному опыту ребенка, при ее решении по необходимости уместно применить практический или графический методы. Такими же методами предлагается решить задачу 1 работы 33.

    Подобные задачи включены и в итоговые работы, которыми заканчивается каждая рабочая тетрадь этой серии. Например, задание 5 Итоговой работы 1 из тетради для 3 класса.

    Следует обратить внимание еще на один важный момент при использовании этих пособий – это встроенность системы формирования навыков самопроверки, самоконтроля и самооценки. После выполнения работы педагог организует этот этап по варианту пособия с ответами и решениями, которые можно скачать с сайта издательства. Ученик проверяет работу и ставит в прямоугольник на полях задания специальную пометку:

    Такая работа позволяет ученику анализировать и оценивать результаты, в случае ошибок планировать работу по исправлению, для этого выделять знания и умения, требующие дополнительного повторения.

    Формированию оценочных умений при работе с заданиями по математике также способствуют пособия серии «Проверь себя». Продолжим иллюстрировать примерами линию работу с нестандартными задачами и обратим внимание на выпущенную в этой серии новинку 2018 года – «Тестовые тренировочные задания. Математика. 3 класс», тетрадь-практикум автора А.Г. Ванцяна.

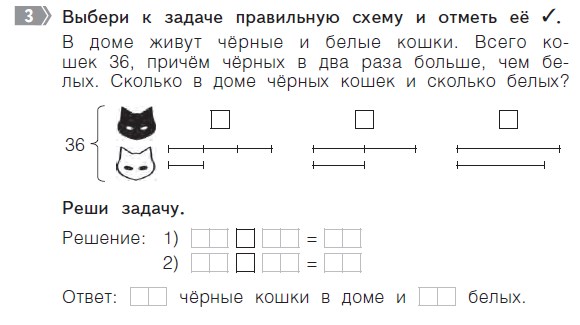
    Задания в этом пособии часто предлагаются от лица сказочных персонажей, тексты носят занимательных характер, что будет способствовать повышению интереса учащихся, стимулировать мотивацию к выполнению. Отличительная особенность пособия – встроенность различных обучающих элементов: учащиеся закрепляют и проверяют умения поэтапно работать с текстовой задачей, анализировать и соотносить условие и вопросы, подбирать соответствующие модели, выбирать решения и ответы. Все это помогает учащимся осваивать основные этапы работы с текстовой задачей, переносить их в новую ситуацию. Подобные задания предлагаем рассмотреть на приведенном выше фрагменте. Кстати, к данному пособию также размещены ответы на сайте.

    Обсуждение пособий по математике в контексте работы с нестандартными задачами будет неполным, если не представить тетради диагностических тестовых работ для начальной школы серии «Контролируемые элементы содержания» (КЭС), разработанные педагогами г. Москвы под редакцией Е.В. Волковой, научный руководитель проекта Н.Б. Фомина.

    Каждая работа тетрадей для 1–4 классов сопровождается методическим инструментарием (планирование, методические комментарии, решения и ответы, система оценивания и обработки результатов, их анализа). Материалы тетрадей позволяют проверить знания учащихся по основным темам курса математики каждого класса, а также провести итоговый контроль в конце учебного года. Диагностические тестовые работы представлены в двух вариантах.

    Приведем несколько примеров заданий из различных диагностических работ, включенных в тетрадь этой серии по математике для 3 класса, авторы Н.В. Буянова, М.С. Сырокомская.

    Приведенные примеры диагностических заданий содержат нестандартные формулировки, проверяют предметные результаты освоения программного материала на повышенном уровне, помогают выявить учащихся, овладевших способом переноса базовых знаний и способов действий в новые условия.

    Таким образом, нестандартные задачи необходимо шире включать в содержание обучения математике в начальной школе в качестве средства реализации ее развивающего потенциала. Издательский дом «Федоров» стремится поддержать желание и готовность педагогов использовать их в своей практике (на уроках и во внеклассной работе), разрабатывает для этого пособия и выстраивает методические инструменты работы с ними. Данные пособия будут очень хорошими помощниками родителям, а ученики смогут выстроить с ними самостоятельную работу.

    Учите и учитесь решать нестандартные задачи! Успехов!

    ЛИТЕРАТУРА

1. Кордемский Б.А. Очерки о математических задачах на смекалку. М.: Учпедгиз, 1958.
2. Колягин Ю.М. Учебные математические задания творческого характера // Роль и место задач в обучении математике. М., 1973. Вып. II.
3. Аналитические материалы по результатам проведения Национального исследования качества начального общего образования в 4 классах по предметам: «Русский язык», «Математика», «Окружающий мир». Часть 3. Математика. Федеральная служба по надзору в сфере образования и науки, 2015.