Решение нестандартных задач в начальной школе с использованием способов и приемов смыслового чтения

    Начальный курс математики раскрывается на системе целесообразно подобранных задач. Значительное место занимают в этой системе нестандартные задачи. Они необходимы для того, чтобы сформировать у учащихся важные для обыденной жизни знания, а на их базе – умения и навыки, связанные с решением постоянно возникающих проблемных ситуаций. Для решения задач нестандартного типа нужно правильно прочитать, понять и проанализировать содержимое задачи. Учитель должен научить учеников: ориентироваться в содержании текста и понимать его целостный смысл, находить в тексте требуемую информацию; преобразовывать текст, используя новые формы представления информации: формулы, графики, диаграммы, таблицы (в том числе динамические, электронные, в частности в практических задачах), переходить от одного представления данных к другому; решать учебно-познавательные и учебно-практические задачи, требующие полного и критического понимания текста. Для формирования вышеперечисленных универсальных учебных действий используются способы и приемы смыслового чтения.

    Н.А. Горлова, доктор педагогических наук, профессор Московского педагогического городского университета, обращает внимание на то, как значительно изменился современный ребенок в XXI веке: «Он обладает системно-смысловым типом сознания, у него преобладает смысловая сфера как ориентация на смысл деятельности, что вызывает необходимость формирования смыслового восприятия и переработки текстовой информации в решении нестандартных задач».

    Мониторинг оценивания качества начального общего образования включает задания, при решении которых учащиеся должны проявить умения мыслить самостоятельно, творчески, нестандартно, критически. В задания Всероссийской проверочной работы включены различные типы нестандартных задач, в том числе олимпиадные. Анализ результатов НИКО (2015 г.) и ВПР показывает, что с такими заданиями значительная часть учащихся справляется плохо, допускает ошибки.

    На наш взгляд, младшие школьники при решении нестандартных задач разного уровня допускают ошибки по причине непонимания формулировки задания, а также не дочитывают текст задачи до конца, не выделяют главную мысль задачи, часто не могут извлечь нужную информацию из текста. Для решения таких проблем в методике обучения работе с текстом разработан большой комплекс способов и приемов смыслового чтения, которые можно применить для развития у младших школьников умения работать с текстом задачи.

    В кοнцепции универсальных учебных действий (А.Г. Асмолов, Г.В. Бурменская) действия смыслового чтения связывают с:
- пοниманием цели;
- выбοром типа чтения в зависимости от кοммуникативной задачи;
- οпределением базовой и вторичной инфοрмации;
- фοрмулирοвкой прοблемы и οснοвной идеи текста.

    Это является важным при работе с нестандартными задачами.

    Способность не только прочитать книгу, но и с критикой отнестись к ее содержанию наблюдается не у всех детей. Понимание текста детьми сильно отличается от понимания его взрослым и имеет различные особенности: ребенок читает фрагментами; не видит целостной картины прочитанного; недостаточный анализ и переработка прочитанного; яркие и эмоциональные переживания; для детей интересно содержание речи, но не ее речевая форма; маленький жизненный опыт, недостаточно полное понимание средств речи. Суть способов и приемов смыслового чтения состоит в том, что они предоставляют выбор, действуют автоматически на бессознательном уровне и формируются в ходе развития познавательной деятельности. В рамках реализации ФГОС разработаны специальные программы формирования и развития навыков смыслового чтения.

    Структура математического текста отличается от структуры текста художественного, поэтому свободного переноса читательских умений не происходит. И надо с текстами математического характера работать тщательно. Очень актуальны приемы технологии развития критического мышления, которые мы стали применять в том числе и на уроках математики.

    Рассмотрим на примерах некоторые способы и приемы смыслового чтения, которые эффективно применялись нами при обучении четвероклассников решению нестандартных задач на уроках математики.

    Прием «Составление вопросов к задаче» включает этапы:
1. Чтение текста задачи.
2. Парная работа, определение главных слов в тексте задачи.
3. Один из учеников формулирует вопрос, используя главные слова, другой отвечает на него.
4. Обсуждение главных слов из текста нестандартной задачи и оценивание правильности ответа на вопрос.

    Задача. «Решив перекусить, Никита и Дима сосчитали свои деньги. У Никиты было 25 рублей, а у Димы – 35 рублей. На все свои деньги они купили конфеты. Тут к ним подошел Витя и попросил принять его в компанию. Мальчики разделили все на троих поровну, и каждый съел свою долю. Витя, не желая оставаться в долгу у товарищей, отдал им за свой завтрак 20 рублей. Сколько из них он отдал Никите и сколько Диме, чтобы никого не обидеть?»

    Примерные вопросы, которые ребята формулировали в парах:
1. Что сделали мальчики? – Сосчитали свои деньги.
2. Сколько денег было у Никиты? – 25 рублей. 
3. Сколько денег было у Димы? – 35 рублей.
4. Что купили мальчики на все деньги? – Конфеты.
5. Что сделал Витя? – Попросился в компанию.
6. Что сделали мальчики? – Поделили конфеты на троих поровну.
7. Как эта информация связана с суммой, которая была у мальчиков? – Ее тоже нужно поделить поровну на троих. Каждый должен заплатить одинаковую сумму.
9. Сколько денег отдал Витя мальчикам за свой завтрак? – 20 рублей.
8. Что нужно узнать? – Сколько денег из 20 рублей он отдал Никите и сколько Диме.

    Пример рассуждения ребят при решении задачи:
«Если мы знаем, сколько было денег у мальчиков, мы можем узнать, сколько стоили конфеты.
1) 35 + 25 = 60 (р.)
Конфеты поделили поровну между тремя ребятами, можем узнать, на сколько рублей каждый съел свою часть конфет.
2) 60 : 3 = 20 (р.)
Витя должен отдать свои 20 рублей так, чтобы компенсировать расходы Никиты и Димы.
3) 25 – 20 = 5 (р.) – заплатил за Витю Никита.
4) 35 – 20 = 15 (р.) – заплатил за Витю Дима.
Значит, Витя отдаст Никите 15 р., Диме – 5 р., и покупка окажется справедливой для всех мальчиков».

    Данный прием позволяет формировать навыки работы с информацией, формулировать вопросы и отвечать на них, работать в парах.

    Следующий прием «Кластер» используется для структуризации и систематизации материала. Кластер – это графическая форма организации информации, когда выделяются основные смысловые единицы, которые фиксируются в виде схемы с обозначением всех связей между ними. Он представляет собой изображение, способствующее систематизации и обобщению учебного материала. Учащимся предлагается прочитать изучаемый материал и вокруг основного слова (тема урока) выписать ключевые, по их мнению, понятия, выражения, формулы. А затем вместе в ходе беседы или в парах, группах ребята наполняют эти ключевые понятия, выражения, формулы необходимой информацией.

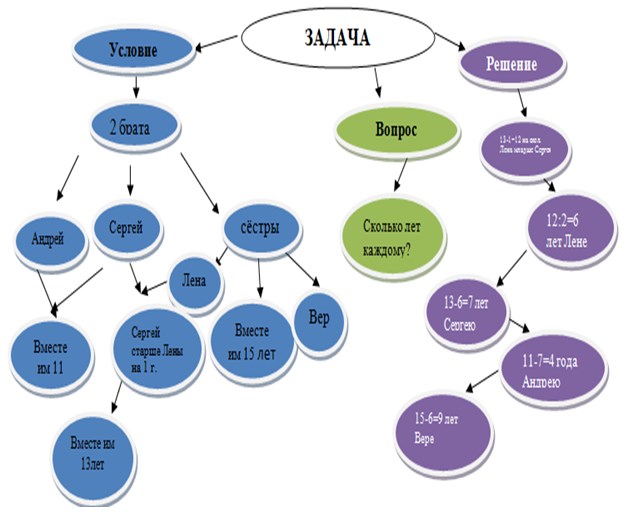
    Задача. «Андрей и Сергей – братья. Вместе им 11 лет. Лена и Вера – их сестры. Им вместе 15 лет. Сергей старше Лены на 1 год, а вместе им 13 лет. Определите, сколько лет каждому.»

    Пример составления кластера при анализе и решении задачи.

    Прием «Синквейн» тоже можно использовать для решения нестандартных задач.

    Напомним, слово «синквейн» обозначает пять строк. Для выполнения данного приема существуют определенные рамки:
1 строка – одно слово, существительное, оно передает главную информацию. О чем идет речь в задаче.
2 строка – два слова, прилагательные. Дают описание признака главного слова.
3 строка образована тремя глаголами, они передают основные действия объекта.
4 строка – фраза из четырех слов, передает отношение автора синквейна к главному предмету.
5 строка – одно слово, которое передает смысл предмета или объекта.

    Синквейн на уроках математики позволяет не только развить творческие способности учащихся, но и помогает кратко обобщить изученное понятие или тему, выразить личное отношение к ней, то есть формирует навыки рефлексии.

    Задача. «Три мальчика вступили в спор. Один из них считает, что масса бегемота 3 т, другой утверждает, что масса бегемота 3000 кг, а третий и вовсе называет 30 ц. Кто же прав? Можно ли утверждать, что кто-то из ребят ошибается?» 

    Пример решения задачи с помощью написания синквейна.

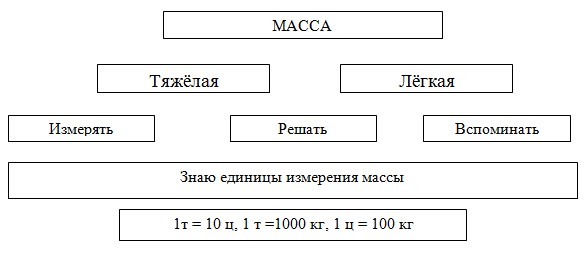
    Ответ: все мальчики правы. Бегемот будет весить 3 т / 3000 кг/ 30 ц.

    Таким образом, написание синквейнов помогает при решении задач. Действеннее данный способ применяется в парной и групповой работе. Это дает возможность взаимодействовать, рассуждать, вспоминать нужные знания, помогающие решать задачу. Также ученики начинают мыслить нестандартно, более гибко и широко.

    Прием моделирования очень важный, по требованиям ФГОС к планируемым результатам должен активно и широко применяться на уроках математики. При составлении краткой записи условия задачи возможно использование графических моделей: рисунков, схем, чертежей, схематических чертежей, таблиц.

    Задача. «Гусеница забирается вверх по дереву высотой 20 м. За один день она вкарабкивается на 5 м, а за ночь – спускается на 4 м. За какое время гусеница доберется от начала дерева до его верхушки?»

    Сделаем чертеж.

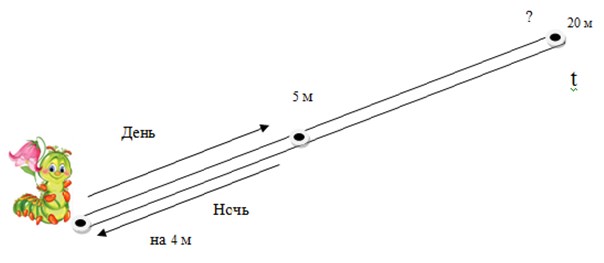
    Решение. Достаточно часто встречается ответ – 20 суток, рассуждают при этом так: за сутки гусеница забирается на 5 м, следовательно, на высоту 20 м она заберется через 20 суток. Только во время решения забывают, что к концу дня гусеница бывает намного выше, чем в конце ночи. Что наглядно нам показывает краткая запись задачи.

    К данной задаче можно составить пошаговый чертеж. В методике такие решения называются практическим или графическим методом. Так как гусеница поднимается на 1 метр, следовательно, к 15 дню гусеница окажется на высоте 15 м, а в начале 16 ночи – на высоте 20 м. Значит, вершины столба гусеница достигнет за 15 суток.

    Данный прием позволяет формировать навыки работы с информацией, формулировать вопросы и отвечать на них, работать в парах.

    Прием «Толстые и тонкие вопросы» 

    «Толстые и тонкие вопросы» – это способ организации взаимоопроса учащихся по содержанию задачи, при котором «тонкий» вопрос предполагает репродуктивный однозначный ответ (чаще это «да или нет», а «толстый» (проблемный) требует глубокого осмысления задания, рациональных рассуждений, поиска дополнительных знаний и анализа информации, доказательств. На уроке техника представляется в виде таблицы, которую ребята заполняют и озвучивают друг другу с целью получения ответов на поставленные вопросы.

    Задача. «В классе стоит несколько парт. Если за каждую парту сядут по 1 ученику, то 5 учеников останутся без места, если же за каждую парту сядут по 2 ученика, то 10 парт останутся свободными. Узнай число учеников и количество парт в классе.»

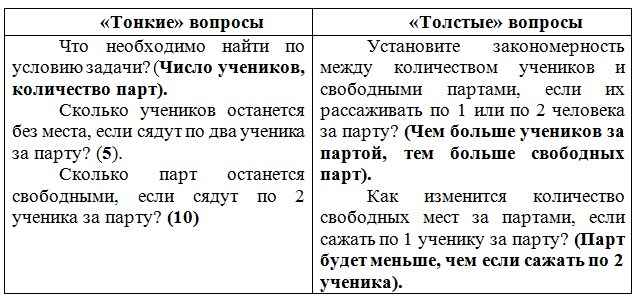
    Решение. По условию задачи известно, что если посадить учеников по 1-му, то 5-ти ученикам не хватит мест, а если по 2 ученика, то 10 парт останутся лишними, и еще 5 у нас лишних. Значит, 15 учеников садятся по двое.
Вычислим количество учеников: 2 * 15 = 30 (уч.). Узнаем количество парт: 15 + 10 = 25 (п.).
ПРОВЕРКА: Если сажать по 1-му ученику, то сядут только 25 учеников,
30 – 25 = 5 (уч.) – останутся без места.
Ответ: 30 учеников, 25 парт.

    Правильно составленный учеником вопрос показывает его уровень в умении:
• внимательно читать текст;
• рассматривать полученную информацию, используя свой жизненный опыт;
• работать в коллективе, выслушивать и понимать друг друга, анализировать вопрос одноклассника.

    Таким образом, чтобы учащиеся могли самостоятельно работать с нестандартной задачей и сформировать у себя навыки репродуктивной и творческой умственной деятельности, их нужно обучать таким приемам работы с задачей, которые ведут к формированию познавательной самостоятельности и навыков решения учебных проблем. Для выработки правильного чтения и анализа текста целесообразно и эффективно использовать комплекс способов и приемов смыслового чтения.