Учим решать текстовые задачи с помощью моделирования
- Автор: Ю.А. Коломасова, педагог, г. Тюмень, О.В. Федоскина, к.п.н., методист отдела повышения квалификации, методических и инновационных проектов ИД «Федоров», доцент кафедры психологии и педагогики детства ИПиП ТюмГУ, автор учебных пособий
Математика оказывает значительное влияние на темпы роста научно-технического развития страны. Поэтому в условиях стремительного технического прогресса необходимы специалисты, владеющие математическими знаниями и умениями, что подчёркивается в «Концепции развития математического образования в Российской Федерации» [1].
Главной и неотъемлемой частью курса математики является решение текстовых задач. Анализ проведенных за последние годы Всероссийских проверочных работ по математике показывает, что этот раздел математики вызывает значительные трудности у младших школьников. Поразмышляем, как моделирующая деятельность в ходе анализа задачи помогает достичь более эффективных результатов обучения решению текстовых задач в начальной школе.
В начальном курсе математики под текстовой арифметической задачей понимается некий специальный текст, в котором обрисована житейская ситуация, охарактеризованная численными компонентами. Ситуация обязательно содержит определенную зависимость между этими численными компонентами. «Математическая модель – это описание какого-либо реального процесса на математическом языке» (Демидова Т.Е., Тонких А.П.) [3].
Решение текстовых задач с помощью моделирования развивает математическое мышление, воображение, смекалку, творчество, умения и навыки, положительно влияющие на умственные способности и личностные качества младших школьников, а также формирует навык поиска решений трудных житейских задач, учит принимать решения, логически мыслить. Федеральный государственный образовательный стандарт начального общего образования в требованиях к результатам освоения основной образовательной программы зафиксировал моделирование как значимое метапредметное УУД: «использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач [2].
Методика обучения моделированию текстовых задач включает следующие этапы:
I этап – подготовительная работа к моделированию текстовых задач;
II этап – обучение моделированию текстовых задач;
III этап – закрепление умения решать задачи с помощью моделирования.
Подготовительная работа начинается еще до начальной школы и продолжается в первом классе. Для этого надо развить необходимые умения и навыки:
- визуализации (восприятия и представления сюжета и выявления зависимостей);
- графические навыки, умения пользоваться линейкой и карандашом (чертить отрезки, выделять равные отрезки, прямые линии, ставить точки);
- зрительное восприятие (сравнение отрезков, их длин на глаз).
На втором этапе знакомим детей с видами моделей и умением их использовать в соответствии с условиями задачи.
Цель третьего этапа – зафиксировать умения и научиться применять их на практике.
Все применяемые модели делятся на две основные группы: схематизированные и знаковые. Такое деление неслучайно, оно опирается на характеристики типов мышления младших школьников. Решение задач начинается с опоры на наглядно-действенное мышление, переходит в наглядно-образное мышление, и по мере развития детей действия и образы уступают свое место понятиям и выражениям. При решении задачи уже не требуется наглядность, т.к. мышление переходит на новый уровень, становясь словесно-логическим.
Итак, моделирование в обучении математике служит методическим средством, а именно средством формирования у обучающихся математических понятий и привития им умений выполнять математические действия, а также использования моделей как внешних опор для организации мыслительной деятельности, в том числе при решении текстовых задач. Решение любой задачи арифметическим методом связано с выбором арифметического действия, в результате выполнения которого можно дать ответ на поставленный вопрос. Чтобы облегчить поиск математической модели, необходимо использовать вспомогательные модели различных видов (рисунок, краткая запись, таблица, чертеж, граф и другие).
Перечислим некоторые методы и приемы работы, способствующие формированию умения решать текстовые задачи с помощью моделирования:
1. Внимательное прочтение текста задачи.
2. Первичный анализ текста задачи, возможен и повторный анализ, хотя это занимает время, но дает хорошие результаты:
• Постановка вопроса к условию;
• Выбор условия к вопросу;
• Составление условия к вопросу;
• Выбор условия и вопроса;
• Выбор схемы к данной задаче.
3. Преобразование анализа в модель.
4. Использование разных моделей для одной текстовой задачи.
5. Анализ построенной модели.
6. Осуществление перехода от построенной модели к тексту.
7. Составление различных путей решения одной задачи.
8. Составление различных выражений по данным задачи; объяснение, что обозначает то или иное готовое выражение; выбор тех выражений, которые являются ответом на вопрос задачи.
9. Сравнение нескольких задач.
10. Запись нескольких решений одной задачи на доске с разыми моделями, разными решениями, возможно верное и неверное решение одной задачи.
11. Изменение вопроса задачи без изменения условия; изменение условия без изменения вопроса; изменение и того, и другого, ранее решенной задачи.
12. Изменение условия задачи таким образом, чтобы она решалась другим действием (косвенные задачи) или несколькими действиями.
13. Выбор правильного решения и его завершение.
14. Определение лишнего или недостающего действия в задаче.
15. Составление аналогичной задачи с измененными данными.
16. Составление аналогичной задачи от модели к тексту с последующим ее решением.
Проиллюстрируем описанное примерами заданий из пособий по математике для учащихся начальной школы Издательского дома «Федоров», которые позволяют как обучать моделированию при решении задач, так и организовать диагностику умений. При этом задания способствуют развитию осознанности и оценочной самостоятельности младших школьников, готовят к успешному написанию различных контрольно-диагностических работ.
Примеры из пособия «Математика 3 кл. Тестовые тренировочные задания. Тетрадь-практикум» (авт. А.Г. Ванцян)


Примеры из пособия «Математика. 3 класс. Готовимся к Всероссийским проверочным работам. 50 шагов к успеху» (авт. А.Г. Ефремова)
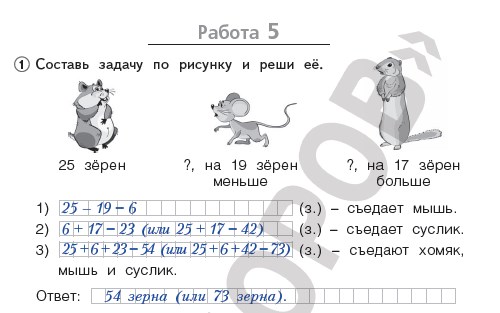
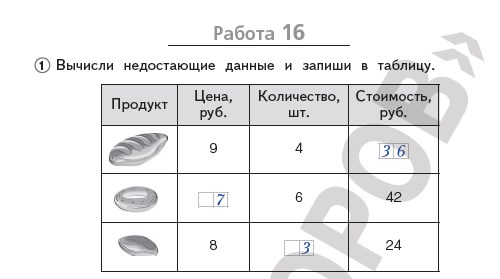
Примеры заданий из тетради «Что я знаю. Что я умею. Математика. 3 класс» (авт. Л.А. Иляшенко)
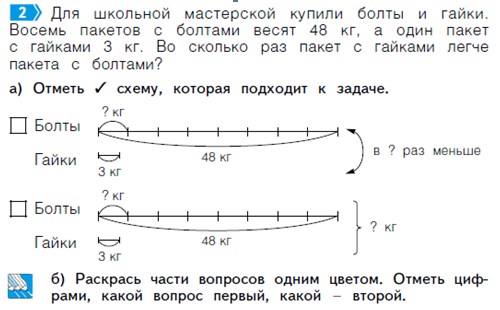
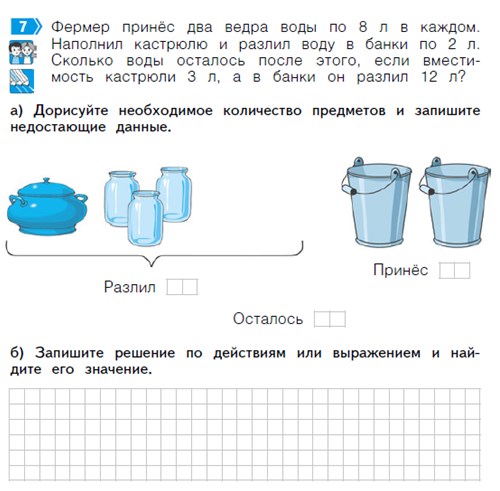
В завершении несколько рекомендаций и советов.
1. Решение любой, даже самой трудной, задачи подчиняется главному закону: по двум данным находим третье.
2. Если ребенку трудно составить краткую запись, попробуйте дать ему задачу, которая содержит лишние сведения. Пускай ученик вычеркнет все ненужное.
3. Если с переходом к составным задачам возникли трудности при их решении, попробуйте выполнять следующие действия:
• вернитесь к простым задачам, но «другой дорожкой». Пусть ученики пробуют составлять всевозможные типы задач к выражениям, содержащим одно действие;
• попробуйте решить задачу, в которой не хватает данных.
4. Обязательно использование системного подхода при решении текстовых задач. Стремитесь к тому, чтобы ни одна задача не оставалась без модели, при этом давайте ученикам свободу выбора модели, поощряйте самостоятельность, развивайте осознанность.
Советы при обучении младших школьников решению задач в курсе математики
1. Задачу необходимо читать ребенку не менее двух раз. Обязательно убедитесь, понял ли он ее содержание, владеет ли понятиями. Если нет, то вначале покажите, объясните, что эти слова значат.
2. Даже если ребенок ответил правильно, задачу нужно проанализировать и задать ребенку наводящие вопросы: что нужно делать? почему так получилось? как ты решал?
3. Вы можете менять числа в задачах в соответствии с возможностями учащихся.
4. Решать задачи следует не более 15 минут несколько раз в день в зависимости от возраста учащегося.
5. За каждую самостоятельно решенную задачу поощряйте ученика.
6. Составляйте с детьми новые задачи и решайте их.
Таким образом, формирование у младших школьников умения решать текстовые задачи – сложный и длительный процесс, требующий большого труда и применения разнообразных подходов и видов деятельности. Один из таких – моделирование. Необходимо обучать применению различных видов моделей при решении текстовых задач, делать это осознано и системно, тогда будет расти качество успеваемости всего класса при решении текстовых задач, ученики будут более самостоятельными, уверенными и успешными.
ЛИТЕРАТУРА
1. Концепция развития математического образования в Российской Федерации // Министерство образования и науки Российской Федерации. М., 2013. – 9 с.
2. Федеральный государственный образовательный стандарт начального общего образования // Министерство образования и науки Российской Федерации. М., 2010. – 31 с.
3. Демидова Т.Е. Теория и практика решения текстовых задач. М., 2002. – 288 с.
